Durée
1 an
Composante
UFR de mathématiques et informatique (UFR27)
Présentation
Programme
Sélectionnez un programme
ERASMUS Mathématiques
Facultatif
Advanced process engineering and process modelling
30hAnglais
2 crédits30hArchitecture des systèmes informatiques
30hArchitectures logicielles et Web
4 crédits30hAtelier "Créativité et innovation"
18hAtelier "Veille technologique"
18hComptabilité & comptabilité analytique
30hContrôle de gestion
20hCours extérieur (Université Paris 1)
4 créditsDecisional systems
30hDroit
20hFLE SGEL
3 créditsFondement de l'Algorithmique
30hFrameworks, composants métiers et Web service
5 crédits40hGestion de projet avancée
4 crédits30hGraphes et algoritmes
30hInformatique décisionnelle
30hIngénierie avancée des processus
30hIngénierie de développement des IHM
30hIngénierie des exigences
30hMarketing digital
20hMéthodes de recherche
30hMéthodes d'ingénierie des SI: Fondamentaux
30hMéthodes statistiques
30hModel driven engineering and model quality
30hModèles de l'ingénierie des SI
4 crédits30hProgrammation orientée objet (POO)
30hRequirement engineering
30hResearch Methods
30hRéseaux
30hSéminaire thématique
12hTechniques de communication
12hTechniques de communication
15hTechniques de test et validation du logiciel
30hVariabilité, ligne de produits et fabrique logicielle
30hVariability, Software product lines and factories
30h
Facultatif
Analyse
4 crédits42hAnalyse réelle 2
8 crédits66hAnalyse S5
72hBanque et marchés
4 crédits36hCorporate finance
42hCorporate Finance (Finance d'entreprise)
4 crédits42hCours extérieur (Université Paris 1)
4 créditsCulture & compétences numériques
2 crédits21hEconométrie 1
4 crédits42hEconomie descriptive
24hFLE
48hFLE SGEL
3 créditsFLE 1
48hFondements des mathématiques
7 crédits54hInformatiques S1
4 crédits36hInformatiques S3
4 crédits36hIntégration & Probabilité
78hIntroduction aux théories économiques
42hIntroduction générale à l'économie
36hIntroductory finance
42hLinear Algebra
42hMacroeconomics 1a
42hMacroeconomics 1b
42hMacro-économie
4 crédits36hMacroéconomie
48hMécanismes monétaires
36hMéthodologie économie
2 crédits18hMicroeconomics 1a : individual decision making
42hMicroeconomics 1b : Equilibria & optimality
42hMultivariable Calculus
42hProbabilités 1
4 crédits42hProbability and statistics
84hProgrammation linéaire
42hProgrammation orientée objet
4 crédits36hStatistiques 1
54hStatistiques 1
36hTechnique du calcul
48h
Facultatif
Algorithmique avancée
4 crédits30hAnglais (préparation certification)
30hArchitecture Orientée Objet
30hAteliers "outils de développement mobiles"
9hBases de données non SQL
4 crédits30hBases de la RO et de l'optimisation
30hCloud & pervasive computing
30hCloud & pervasive computing
30hContraint reasoning and its applications
30hCours extérieur (Université Paris 1)
4 créditsData Mining & Big Data
30hFLE SGEL
3 créditsFouille de processus
30hGestion de projets: Fondamentaux
30hIngénierie & management de la connaissance
30hInitiation aux stratégies d'entreprises dans les TIC
2 crédits20hIS quality and security
30hKnowledge engineering and management
30hModèles et outils pour les processus
4 crédits30hModélisation événementielle et ses implémentations
4 crédits30hOutils d'analyse de documents structurés
4 crédits30hProcess mining
30hProjet commun ou concours
5hProjet commun ou concours
5hRaisonnement par contraintes et ses applications
30hRessources Humaines et Marketing
30hSécurité & qualité des SI
30hTechniques de communication
12hTechniques de communication
15hTechniques mathématiques pour l'aide à la décision
30h
Facultatif
Algèbre linéaire 1
7 crédits54hAlgèbre linéaire 2
54hAnalyse dans Rn
54hAnalyse de données
4 crédits42hAnalyse réelle 1
7 crédits54hApplied Econometrics
42hAssurance: théorie & pratique
4 crédits42hComplément de calcul intégral et différentiel
4 crédits36hCours extérieur (Université Paris 1)
4 créditsDynamique
4 crédits42hEconométrie 2
4 crédits42hFLE
48hFLE SGEL
3 créditsFLE 2
48hInformatique S4
4 crédits36hInformatiques S2
4 crédits36hIntroduction au calcul des variations
4 crédits42hIntroduction aux logiciels statistiques
4 crédits24hMacroeconomics 2a
27hMacroeconomics 2b
27hMarchés Equilibre et Optimum
4 crédits42hMéthodes Numériques
4 crédits42hMicroeconomics 2 (Mathematical game theory)
54hMicroeconomics 3 (information economics)
42hMicroéconomie 1
4 crédits36hMicroéconomie 2
4 crédits42hModèles mathématiques en finance
4 crédits42hOptimisation
8 crédits60hOptimisation combinatoire
4 crédits42hPolitique économique
4 crédits36hPortfolio Choice and Asset Pricing
42hProbabilistics methods in finance
42hProbabilités 1
6 crédits48hProbability 2
42hStatistics A: euclidean algebra
42hStatistics B
42hStatistiques 2
4 crédits42hStatistiques 2
8 crédits60hTheory in finance
42h
Advanced process engineering and process modelling
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
In the first part of the class, we discuss intention-oriented paradigm for process modeling. The meta-model MAP is used to explore intentional process modeling and we apply it in different case studies.
In the second part of the class, we discuss activity-oriented and state-oriented paradigms for process modeling. We discuss state machines and statecharts modeling for system specification. We define the limits of BPM and examine how the state-oriented paradigm can overcome these limits. We use YAKINDU statecharts tool for process modeling and simulation.
Keywords: Intentional process modeling; Product/Process; State machine; Statechart; Case management process
Anglais
ECTS
2 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Architecture des systèmes informatiques
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Architectures logicielles et Web
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Atelier "Créativité et innovation"
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
18h
Période de l'année
Automne
Atelier "Veille technologique"
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
18h
Période de l'année
Automne
Comptabilité & comptabilité analytique
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Contrôle de gestion
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
20h
Période de l'année
Automne
Cours extérieur (Université Paris 1)
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Période de l'année
Automne
Decisional systems
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Droit
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
20h
Période de l'année
Automne
FLE SGEL
ECTS
3 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Fondement de l'Algorithmique
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Frameworks, composants métiers et Web service
ECTS
5 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
40h
Période de l'année
Automne
- Introduction — What are the roles of a software architect ?
- Software Architecture : a Framework-based approach
- Basics of Software Architecture
- Inversion of Control with Jakarta EE8 – CDI
- Data format Binding with Jakarta EE8 – JAXB
- Rest Architectures and Implementation with Jakarta EE8 — JAXRS
- Persistence with Jakarta EE8 — JPA
- Message-based communication with Jakarta EE8 — JMS
- Business Logic with Jakarta EE8 — EJB
- Software Architecture Design: Enterprise Application Patterns
- Architecture Integration : Enterprise Integration Pattern
Gestion de projet avancée
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Graphes et algoritmes
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Informatique décisionnelle
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Ingénierie avancée des processus
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Ingénierie de développement des IHM
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Ingénierie des exigences
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Marketing digital
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
20h
Période de l'année
Automne
Méthodes de recherche
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Méthodes d'ingénierie des SI: Fondamentaux
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Méthodes statistiques
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Model driven engineering and model quality
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Modèles de l'ingénierie des SI
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Programmation orientée objet (POO)
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Requirement engineering
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Research Methods
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
This class proposes an introduction to Research Methodology.
Weather you plan to pursue your career in a research team (R&D or Academic research team) or in an innovative competitive organisation, research methods allow for informed investigation and decision making in various areas. We will examine different (empirical) methods to be used in Research projects in technology, software engineering and IS domains. 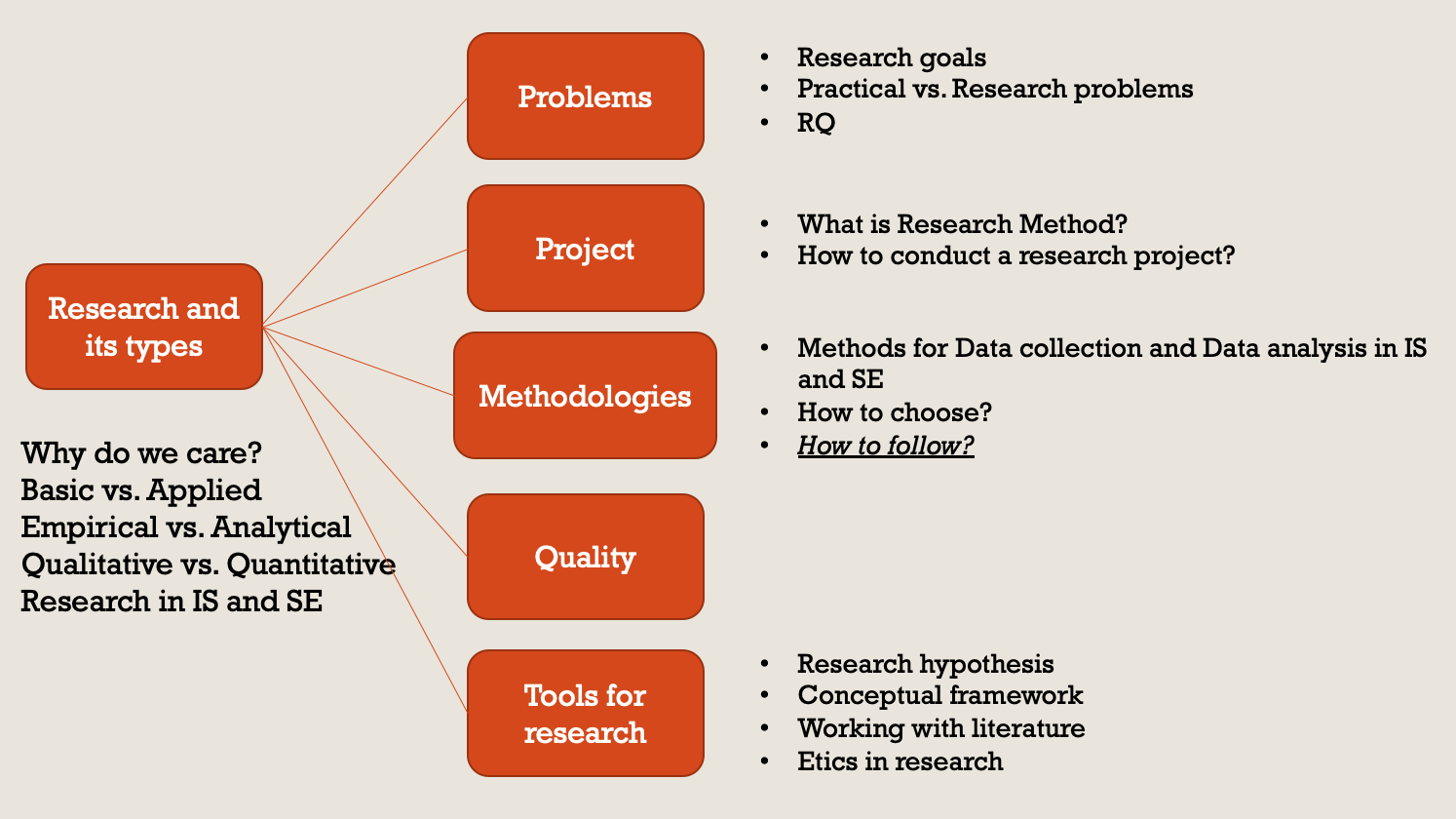
Réseaux
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Séminaire thématique
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
12h
Période de l'année
Automne
Techniques de communication
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
12h
Période de l'année
Automne
Techniques de communication
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
15h
Période de l'année
Automne
Techniques de test et validation du logiciel
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Variabilité, ligne de produits et fabrique logicielle
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Variability, Software product lines and factories
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Analyse
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Objectifs: Acquérir des bases en analyse fonctionnelle.
Contenu du cours:
- Processus diagonal de Cantor.
- Espaces de Banach de dimensions finies et infinies.
- Applications linéaires continues entre espaces de Banach.
- Théorème de points fixe de Banach-Picard.
- Théorème d’Arzela-Ascoli.
- Théorème de Baire.
-Théorème de la projection et théorème de Riesz dans les espaces de Hilbert.
Références:
- Cours d’analyse fonctionnelle avec 200 exercices corrigés (Daniel Li)
- Analyse Fonctionnelle- Théorie et applications (Haim Brezis)
- Analyse pour l’agrégation (Hervé Queffélec, Claude Zuily)
Analyse réelle 2
ECTS
8 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
66h
Période de l'année
Automne
Analyse S5
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
72h
Période de l'année
Automne
Banque et marchés
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Automne
Corporate finance
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Corporate Finance (Finance d'entreprise)
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Objectifs:
Il s'agit d'un cours couvrant les concepts de base de la finance d'entreprise et de la prise de décision financière, tels que l'évaluation en l’absence d’arbitrage et la loi du prix unique, la valeur temps de l'argent, les règles de décision d'investissement, l'analyse des états financiers, l'évaluation de base des actions et des titres à revenu fixe, le modèle d'évaluation des actifs financiers (MEDAF) et les principes fondamentaux de la structure financière d’une entreprise.
Contenu du cours:
Partie 1. Concepts de base (VAN, arbitrage, valeur temps de l'argent)
Partie 2. Analyse des états financiers
Partie 3. Évaluation des obligations et des actions
Partie 4. Risque et rendement : le modèle d'évaluation des actifs financiers (MEDAF)
Partie 5. Structure financière et théorème de Modigliani-Miller
Références:
Corporate Finance (3rd edition), Berk & DeMarzo. Pearson publishing.
Cours extérieur (Université Paris 1)
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Période de l'année
Automne
Culture & compétences numériques
ECTS
2 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
21h
Période de l'année
Automne
Econométrie 1
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Objectifs:
Estimer les paramètres d’un modèle linéaire, expliquer les conditions pour que ces estimations soient de qualité, en mesurer le degré de précision, juger de la validité empirique des présupposés théoriques du modèle et indiquer les précautions d’emploi du modèle estimé.
Contenu du cours:
-- Régression linéaire simple : modèle et estimation, analyse de la variance, coefficient de détermination, test sur la nullité de la pente
-- Régression linéaire multiple : quatre formules fondamentales, colinéarité statistique, algorithmes de construction de modèle ne comprenant que des variables significatives, étude de cas
--Analyse de la variance : analyse de la variance à deux facteurs croisés, test de Fisher, test de Student
Références:
Jean-Marc Azaïs et Jean-Marc Bardet, Le modèle linéaire par l’exemple : Régression, Analyse de la variance et Plans d’expérience illustrés avec R, SAS et Splus. Dunod, 2006.
Virginie Delsart, Arnaud Rys et Nicolas Vaneecloo, Économétrie théorie et application sous SAS. Septentrion, 2009.
Economie descriptive
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
24h
Période de l'année
Automne
FLE
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
48h
Période de l'année
Automne
FLE SGEL
ECTS
3 crédits
Composante
UFR de mathématiques et informatique (UFR27)
FLE 1
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
48h
Période de l'année
Automne
Fondements des mathématiques
ECTS
7 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
54h
Période de l'année
Automne
Informatiques S1
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Automne
Informatiques S3
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Automne
Intégration & Probabilité
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
78h
Période de l'année
Automne
Introduction aux théories économiques
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Introduction générale à l'économie
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Automne
Introductory finance
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Linear Algebra
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Macroeconomics 1a
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Objectifs:
Le cours décrit l’histoire de l’élaboration du cadre utilisé aujourd’hui pour décrire la dynamique de l’économie. Il insiste sur le rôle crucial joué par l’accumulation du capital pour rendre compte de la croissance exceptionnelle du produit par tête qu’ont connu les économies occidentales à partir du 19e siècle. Après avoir décrit le comportement d’accumulation du capital par les entreprises, il présente les modèles de croissance dans lesquels l’offre de capital obéit à une logique keynésienne, puis conclut le cours par une première intégration d’un comportement d’épargne optimal. Il n’y a pas de prérequis.
Contenu du cours:
- Faits stylisés de la croissance économique
- L’accumulation du capital
- La décomposition de la croissance
- La croissance en déséquilibre : l’approche de Harrod-Domar
- Le modèle de Solow
- Le modèle de cycle de vie
Références:
Blanchard, O. et D. Cohen, Macroéconomie, Pearson, 8e édition, 2020
Macroeconomics 1b
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Objectifs:
Le cours suit Macroeconomics 1A et présente les deux principaux cadres d’analyse des modèles de croissance que l’on utilise aujourd’hui pour discuter l’impact dynamique de politiques économiques : le modèle de croissance optimal (Ramsey-Cass-Koopmans) et le modèle à générations imbriquées.
Contenu du cours:
- Le sentier de consommation optimal : l’équation d’Euler
- La dynamique optimale : Règle d’or modifiée
- Les théorèmes de l’économie du bien-être
- Générations imbriquées et inefficacité de l’équilibre
Références:
Gauthier, S., Macroéconomie, Economica, 2012.
Macro-économie
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Automne
Macroéconomie
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
48h
Période de l'année
Automne
Mécanismes monétaires
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Automne
Méthodologie économie
ECTS
2 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
18h
Période de l'année
Automne
Microeconomics 1a : individual decision making
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Objectifs:
Ce cours est un cours de microéconomie mathématique. Il porte sur les comportements rationnels et les prises de décisions des consommateurs et des producteurs. Il se concentre d’abord sur les résultats fondamentaux des théories de la demande Walrasienne, des préférences révélées et des décisions dans l'incertain. Ensuite, quant au producteur, l'objectif est d’analyser deux comportements classiques, c.-à-d. la maximisation du profit et la minimisation des coûts, et les liens entre les deux. Les méthodes mathématiques utilisées vont de la topologie, à l'analyse et l'optimisation sous contraintes.
Contenu du cours:
- Préférences, maximisation des préférences sous contrainte budgétaire, demande Walrasienne.
- Structures de choix, préférences révélées, axiome faible de la préférence révélée.
- Théorie de l'utilité espérée, Théorème d'utilité de von Neumann-Morgenstern, paradoxes.
- Ensemble de production, fonction de transformation, fonction de production, propriétés.
- Maximisation du profit, offre du producteur.
- Minimisation des coûts, demande du producteur.
- Liens entre la maximisation du profit et la minimisation des coûts.
Références:
Mas-Colell, A., Whinston, M.D., Green, J., “Microeconomic Theory”, Oxford University Press, 1995.
Microeconomics 1b : Equilibria & optimality
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Multivariable Calculus
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Probabilités 1
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Objectifs:
Ce cours présente les notions fondamentales associées au calcul des probabilités. Il met notamment en œuvre les concepts et les outils étudiés en théorie de la mesure. Il a pour objectif de fournir le bagage théorique nécessaire pour aborder en Master 2 les problématiques de modélisation aléatoire.
Contenu du cours:
- Espace de probabilité et vecteur aléatoire : tribu, mesure, notion de mesurabilité, rappels d’intégration, théorèmes de convergence
- Loi de probabilité : atome, loi à densité (principe de domination), lois marginales, notion d’indépendance, noyau de transition, fonction de répartition
- Espérance mathématique : théorème de transfert, inégalités usuelles, notion d’indépendance.
- Espaces Lp
- Espérance conditionnelle sur une sous-tribu : présentation théorique, propriétés, notion d’indépendance, applications
- Fonctions caractéristiques : théorème d’injectivité et formule d’inversion de Fourier, notion d’indépendance.
- Vecteurs Gaussiens : caractérisations, notion d’indépendance, espérance conditionnelle.
- Convergences : presque sûre, stochastique, au sens Lp
- Convergence en Loi : caractérisations (théorème porte-manteau, Scheffé, théorème de Lévy)
- Théorèmes Limites : Lois de grands nombres, théorème central limite.
Probability and statistics
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
84h
Période de l'année
Automne
Programmation linéaire
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Automne
Objectifs:
Les problèmes d'optimisation avec une fonction objectif et des contraintes linéaires (appelés classiquement "programmes linéaires") constituent une classe importante de problèmes pour lesquels il existe des méthodes de résolution efficaces, en particulier la méthode du simplexe. De plus, la programmation
linéaire constitue l'outil fondamental de résolution des problèmes d'optimisation en recherche opérationnelle, qui ont une grande importance pratique : problèmes d’affectation, transport, production, planification, etc. Elle est aussi étroitement reliée à la résolution des systèmes d'inégalités et aux polyèdres convexes. Le cours se limite aux problèmes avec variables continues. Le cas des variables 0-1 ou entières, très courant en pratique, est traité dans le cours “Optimisation Combinatoire” pour lequel ce cours est un pré-requis.
Contenu du cours:
- Présentation de quelques problèmes pratiques courant en recherche opérationnelle, et modélisation sous forme de programme linéaire.
- Forme standard d'un programme linéaire, interprétation et résolution géométrique.
- La méthode du simplexe, notion de dictionnaire, de solution de base.
- Initialisation du simplexe, méthode à 2 phases, bouclage, temps de calcul.
- Notion de dualité, écarts complémentaires, interprétation économique du dual.
- La méthode révisée du simplexe.
- Solvabilité d'un système d’inégalités linéaires, lemmes de Farkas, élimination de Fourier-Motzkin.
- Analyse de sensibilité.
- Les autres méthodes de résolution (ellipsoïde, méthode du point intérieur)
- Polyèdres et polytopes convexes, sommets et rayons extrêmes
Références:
- Chvatal. Linear programming. W.H. Freeman and Company, 1983.
- Matousek, B. Gärtner. Understanding and using linear programming. Springer Universitext, 2007.
- Gondran, M. Minoux. Programmation mathématique, Théorie et Algorithmes. Dunod, 1983.
Programmation orientée objet
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Automne
Statistiques 1
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
54h
Période de l'année
Automne
Statistiques 1
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Automne
Objectifs:
Le but de ce cours est d’étudier les modèles paramétriques dans un cadre asymptotique. Après un rappel des principaux résultats de convergence, on construira les estimateurs du vecteur paramètre et on donnera leurs propriétés asymptotiques. Il finira par une introduction à la théorie des tests.
Contenu du cours:
- Rappel de probabilités :
- Intégration, variables aléatoires, indépendance
- Convergences. Lemme du porte-manteau.
- Delta-méthode.
- Espérance conditionnelle
- Estimation paramétrique :
- Statistiques exhaustives et complètes, famille exponentielle. Critères d’optimalité.
- Méthode des moments.
- Maximum de vraisemblance
- M-estimateurs.
- Régions de confiance, tests paramétriques et introduction à la sélection de modèles.
Références:
- Saporta, G., Probabilités, analyse des données et statistiques. Technip. 1990
- van der Vaart, A.W. Asymptotic statistics Cambridge series in statistical and probabilistic mathematics, Cambridge University Press. 1998
Technique du calcul
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
48h
Période de l'année
Automne
Algorithmique avancée
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Anglais (préparation certification)
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Architecture Orientée Objet
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Ateliers "outils de développement mobiles"
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
9h
Période de l'année
Printemps
Bases de données non SQL
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Bases de la RO et de l'optimisation
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Cloud & pervasive computing
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Cloud & pervasive computing
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Contraint reasoning and its applications
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Cours extérieur (Université Paris 1)
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Période de l'année
Printemps
Data Mining & Big Data
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
FLE SGEL
ECTS
3 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Fouille de processus
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
La fouille de processus analyse des logs informatiques pour en déduire le comportement des utilisateurs. C'est un domaine au croisement du data mining et de l'approche processus qui permet d'analyser les données des processus opérationnels au niveau de l’ensemble du Système d’Information. Il permet ainsi d’appréhender les processus tels qu’ils se déroulent réellement dans l’organisation
Gestion de projets: Fondamentaux
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Ingénierie & management de la connaissance
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Initiation aux stratégies d'entreprises dans les TIC
ECTS
2 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
20h
Période de l'année
Printemps
IS quality and security
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Knowledge engineering and management
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Modèles et outils pour les processus
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
In the first part of the class, we discuss intention-oriented paradigm for process modeling. The meta-model MAP is used to explore intentional process modeling and we apply it in different case studies.
In the second part of the class, we discuss activity-oriented and state-oriented paradigms for process modeling. We discuss state machines and statecharts modeling for system specification. We define the limits of BPM and examine how the state-oriented paradigm can overcome these limits. We use YAKINDU statecharts tool for process modeling and simulation.
Keywords: Intentional process modeling; Product/Process; State machine; Statechart; Case management process
Modélisation événementielle et ses implémentations
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Outils d'analyse de documents structurés
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Process mining
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Process Mining analyzes computer logs to deduce user behavior. It's a domain at the crossroads of data mining and processes to analyse operational process data at the information system level. This allows to understand the processes as they really take place in the organisation.
Projet commun ou concours
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
5h
Période de l'année
Printemps
Projet commun ou concours
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
5h
Période de l'année
Printemps
Raisonnement par contraintes et ses applications
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Ressources Humaines et Marketing
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Sécurité & qualité des SI
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Automne
Techniques de communication
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
12h
Période de l'année
Printemps
Techniques de communication
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
15h
Période de l'année
Printemps
Techniques mathématiques pour l'aide à la décision
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
30h
Période de l'année
Printemps
Algèbre linéaire 1
ECTS
7 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
54h
Période de l'année
Printemps
Algèbre linéaire 2
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
54h
Période de l'année
Printemps
Analyse dans Rn
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
54h
Période de l'année
Printemps
Analyse de données
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Objectifs:
- L’objectif du cours est d’introduire les fondements et principales questions et approches qui interviennent de façon incontournable dans tous les cours ultérieurs du M2 MMMEF, M2MO ou du M2 TIDE où l’Apprentissage Statistique (machine learning), la Data Science et l'intelligence artificielle apparaissent en bonne place.
- Les séances alterneront entre cours magistraux et séances de travaux dirigés selon l’avancement et en fonction des besoins.
-Les supports de cours (slides) seront en anglais. Cette langue est en effet, qu'on le veuille ou non, un outil indispensable pour acquérir et transmettre des savoirs/informations dans le monde professionnel. Sa maîtrise (au moins pour le vocabulaire technique) est donc devenue indispensable à quiconque envisage une carrière dans le domaine de la Data Science ou de l'Intelligence Artificielle.
Prérequis:
-avoir suivi des cours en théorie des probabilités
-avoir suivi des cours en algèbre linéaire
Contenu du cours:
- Linear regression:
rappels d’algèbre linéaire, décomposition SVD, description du modèle, estimation des paramètres par minimisation du risque empirique/maximisation de la vraisemblance, l’hypothèse gaussienne. - Model selection:
Sur la base du modèle de régression linéaire, on envisage plusieurs modèles candidats.
On introduit l’idée de quantification de la performance et justifie l’utilisation de critères pénalisés de type AIC. La procédure de validation-croisée sera également détaillée. - Classification:
Différents types de modèles seront envisagés tels que la régression logistique, l’analyse linéaire discriminante, le classifieur des k plus proches voisins. - Clustering:
Nous envisagerons différentes stratégies pour définir des mesures de similarité et étudierons deux principales approches pour le clustering : les K -means et le clustering hiérarchique ascendant. - Data Visualization:
Afin de pouvoir visualiser les résultats de l’analyse, nous envisagerons deux principales techniques de réduction de dimension telles que l’analyse en composantes principales et l’analyse canonique des corrélations. La question de l’estimation de densité par estimateurs histogramme ou à noyau sera détaillée.
Références:
-Hastie, Tibshirani, Friedman. The elements of statistical learning: Data Mining, Inference and Prediction. Springer series in Statistics.
Analyse réelle 1
ECTS
7 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
54h
Période de l'année
Printemps
Applied Econometrics
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Assurance: théorie & pratique
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Complément de calcul intégral et différentiel
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Printemps
Cours extérieur (Université Paris 1)
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Période de l'année
Printemps
Dynamique
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Objectifs: le but de cet enseignement est de fournir les outils pour l’étude des phénomènes qui évoluent au cours du temps, de manière continue et déterministe (non aléatoire). L’outil de base est l’étude des équations différentielles. Ce cours vise non seulement à compléter la formation de L3 MIASHS de Paris 1 en faisant l’étude de ces notions habituellement faites en Licence et non vues à Paris 1 (théorème de Cauchy-Lipschitz, méthodes de résolution classiques), puis à donner des techniques qualitatives d’études, qui sont donc plus spécialisées. Une initiation aux techniques qualitatives est d’autant plus nécessaire que la plupart des équations n’admettent pas de solution calculable explicitement. Ce cours est un prérequis pour l’étude de tous les phénomènes qui évoluent au cours du temps (dynamique économique), et plus généralement les équations différentielles interviennent dans de nombreux champs d’application des mathématiques.
Contenu du cours: nous étudierons les équations différentielles : notion de solution approchée, méthode d’Euler (explicite), théorème d’existence et d’unicité des solutions (Peano et Cauchy-Lipschitz), étude dans le cas linéaire, quelques techniques de résolution (équations linéaires, séparation des variables). Initiation aux techniques qualitatives (théorème des bouts, méthodes de barrière). Nous étudierons ensuite le cas particulier des équations autonomes (qui ne dépendent pas du temps)
Econométrie 2
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
FLE
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
48h
Période de l'année
Printemps
FLE SGEL
ECTS
3 crédits
Composante
UFR de mathématiques et informatique (UFR27)
FLE 2
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
48h
Période de l'année
Printemps
Informatique S4
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Printemps
Informatiques S2
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Printemps
Introduction au calcul des variations
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Introduction aux logiciels statistiques
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
24h
Période de l'année
Printemps
Macroeconomics 2a
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
27h
Période de l'année
Printemps
Macroeconomics 2b
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
27h
Période de l'année
Printemps
Marchés Equilibre et Optimum
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Méthodes Numériques
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Microeconomics 2 (Mathematical game theory)
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
54h
Période de l'année
Printemps
Objectifs: Provide the basic concepts of game theory and acquire the methods to model and solve rigorously strategic situations. The course stresses the mathematics of the models. Every concept is illustrated by exercises.
Contenu du cours:
- Strategic games, domination, dominant strategies, sophisticated equilibria, Pareto solutions
- Two-Player Zero-sum games: guaranteeing and defending, maxmin, minmax, value, prudent strategies, optimal strategies, saddle points
- Nash equilibrium, Best reply correspondence, fixed point, existence
- Extensive form games, Strategic associated games and subgames,
- sequential rationality, backward induction, subgame perfect equilibrium, relation to sophisticated equilibrium
- Mixed strategies, mixed extension of a game, characterisation of Nash equilibria, calculations of Nash equilibria.
Références: books by:
-Moulin,
-Osborne and Rubinstein,
-Myerson,
Microeconomics 3 (information economics)
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Microéconomie 1
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Printemps
Microéconomie 2
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Modèles mathématiques en finance
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Optimisation
ECTS
8 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
60h
Période de l'année
Printemps
Optimisation combinatoire
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Objectifs:
De nombreux problèmes concrets requièrent des solutions à valeurs entières (par exemple problèmes de transport, problèmes d'affectation, problèmes d'optimisation où l'on doit déterminer un nombre d'individus, un nombre d'avions,...). Pour de tels problèmes on ne peut pas utiliser les méthodes classiques de la programmation linéaire. On a besoin de méthodes spécifiques aux PLNE (programmes linéaires en nombres entiers).
On commencera par étudier des exemples de modélisation sous la forme de PLNE. Nous verrons que la modélisation de certaines contraintes peut aussi nécessiter l'introduction de variables entières. Nous verrons ensuite les principales méthodes de résolution de ces problèmes.
Contenu du cours:
- Modélisation de problèmes d’optimisation en nombres entiers
- Méthodes par séparation et évaluation
- Méthodes par programmation dynamique
- Méthode des coupes de Gomory
Références:
Sakarovitch, Optimisation combinatoire : méthodes mathématiques et algorithmiques
Politique économique
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
36h
Période de l'année
Printemps
Portfolio Choice and Asset Pricing
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Probabilistics methods in finance
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Objectifs : Option pricing in discrete and continuous time, with martingales use and first steps of stochastic calculus.
Contenu du cours :
Chapter I. Preliminaries
1. Derivative products, description and use: Forward/Future contracts, Options
2. Rates and discounting
3. Arbitrage methods
Chapter II. Forward contracts pricing (reminder, in tutorial)
Chapter III. Mathematical tools
1. Conditional expectation, martingale.
Chapter IV. Option pricing in discrete time
1. N periods binomial model (Cox-Ross-Rubinstein); self-financing strategies,
2. risk-neutral probability, martingale property of the discounted price process,
3. option pricing, delta hedging.
Chapter V. Option pricing in continuous time: Black-Scholes model
1. Brownian motion and Ito processes.
2. Quadratic variation of the Brownian motion,
3. Ito integral for a simple process,
4. Extension to the computation of ∫BtdBt,
5. Ito lemma (heuristic proof).
6. Black-Scholes model
7. Partial differential equation approach, hedging from that equation.
8. Probabilistic approach for European options,
9. Girsanov theorem (particular case),
10. Black Scholes formula, delta computation, use.
Références :
- Hull, Options, futures, and other derivative securities, Prentice-Hall (2018: 10th ed).
- Baxter, M. and Rennie, A., Cambridge University Press, 1996.
- Kwok, Y.K., Mathematical models of financial derivatives, Springer, 2nd edition, 2008 (3 first chapters).
- Jacod, J., Protter, P. (2000) Probability Essentials. Springer.
Probabilités 1
ECTS
6 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
48h
Période de l'année
Printemps
Probability 2
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Objectifs: Martingales and Markov chains in discrete time
Prerequisite: Probability with measure: σ-fields, measure space, measurable maps. Non-negative measures, integration of real valued functions. Convergence of sequences of real valued maps. Monotone convergence, Fatou lemma, dominated convergence (Lebesgue). Lp spaces. Probability measure. Random variables. Expectations of r.v. Independence of sub-σ-fields, independence of random variables.
Contenu du cours:
- Conditional expectation, definition, properties
- Discrete time processes, filtration, stopping time, Sigma-field of events determined prior to a stopping time
- Discrete time Martingales, stopped martingales, optional sampling theorem, maximal inequalities, convergence of martingales, regular martingales
- Markov chains with countable states, conditional independence, Markov property, Markov sequences, transition matrix. Markov chains, communication classes, recurrence and transience, positive states, null states, invariant measures, ergodic properties
References
- Jacques Neveu: Bases Mathématiques de la théorie des probabilités
- Jacques Neveu: Martingales en temps discret
- Lacroix, P. Priouret, Cours: J. Lacroix, Probabilités approfondies, Université Pierre et Marie Curie, Master de Mathématiques, 2005-2006
- Jean Jacod, Chaînes de Markov, Processus de Poisson et Applications, Université Pierre et Marie Curie, DEA de Probabilités et Applications, 2003-2004
Statistics A: euclidean algebra
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Statistics B
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Statistiques 2
ECTS
4 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps
Objectifs:
Ce cours à pour but d’étudier les observations dépendantes de leur passé. D’abord dans un cadre discret, pour dans un cadre continu.
Des applications pratiques se feront avec le logiciel R.
Contenu du cours:
- Introduction aux chaînes de Markov à espace d’états fini.
- Présentation des séries temporelles à observations réelles.
- Equations récurrentes linéaires.
- Modèles ARMA.
- Analyse spectrale.
- Modélisation et prévision d’un processus ARMA
- Modèle SARIMA.
Références:
-P. Brockwell, R. Davis. Time series: Theory and methods. Springer 1991.
-A.W. van der Vaart, Times series, Universiteit Leiden :
https://staff.fnwi.uva.nl/p.j.c.spreij/onderwijs/master/aadtimeseries2010.pdf
Statistiques 2
ECTS
8 crédits
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
60h
Période de l'année
Printemps
Theory in finance
Composante
UFR de mathématiques et informatique (UFR27)
Volume horaire
42h
Période de l'année
Printemps

